yuichi
umakoshi
 |  |  |  |
|---|---|---|---|
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
FIBONACCI
TENSEGRITY
この考え方の起源は、”三平方(ピタゴラス)の定理”で有名な紀元前古代ギリシャのピタゴラス学派(の徽章である星形)に端を発しますが、その頃は「外中比」という言葉が使われていました。「黄金」という”いかにも”という名前をつけたのが誰であるかは、はっきりわかっていません。現在のもっとも有力な説は、19世紀に入ってからの比較的最近のことではないかといわれています。オーム(M.Ohm)が1835年に出版した『「純粋初等数学』のなかに「Goldene(黄金)」という言葉がでてきますので、彼が名付け親かもしれません。(D.E.Smithの『数学の歴史』第2巻による)
「黄金比」はヨーロッパでは古くから最も美しい長方形として親しまれてきました。右図のように、ルーブル美術館に所蔵のミロのビーナス、パリの凱旋門、ギリシャの遺跡パルテノン神殿でこの「黄金比」が利用されています。これら以外にも前述のテレホンカード等の他、画家アングルが描いた「泉」という作品など色々なところに「黄金比」が見られます。
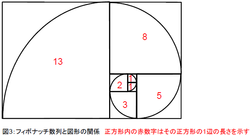
さて、このように黄金比は芸術や建築の世界において多数見出されるとともに、フィボナッチ数列と深い関わりがあるのです。
バックミンスター・フラーはテンセグリティが構造工学における一般的な構造システムのいずれにも分類されないことに気づき、自身の哲学的思想の具体的な表現手段として採用した。テンセグリティは構造システムが破綻しない範囲で、部材を極限まで減らしていったときの最適形状の一種とも考えられている。そのような形状は常識的には三角形を基本単位とするトラスなど単純な幾何学要素の集合であろうと推察されていたから、現代においてもテンセグリティの工学的な視点からの研究は十分ではなく、これからの応用と発展が期待されている。
しばしばバックミンスター・フラーとケネス・スネルソンのいずれが発明者であるかといった議論がなされるが、バックミンスター・フラーのテンセグリティは多面体に類似の対称性の高い形状をしており、一方でケネス・スネルソンのテンセグリティには有機的で不定形な作品が散見され、どちらにも強いオリジナリティが認められる。
テンセグリティは工学においては直線部材のピン接合からなる構造システムのうち、圧縮材が互いに接続されておらず、張力材とのバランスによって成立しているような構造システムである。張力材は互いに接続されていてもよく、3次元構造の場合、圧縮材の両端には3本以上の張力材が少なくとも接続されていなければならない。
圧縮材は、一般的な構造システムにおいて、柱や張力材を突き上げるためのマストとして用いられ、力強く地面に接地している。テンセグリティにおいては圧縮材は、両端に接続された張力材からの張力によりバランスをとり、他と接触しない。張力材はごく細い材料を選択できるから、まるで圧縮材が空中に浮いているかのような印象的な視覚効果を演出できる。そのような背景と、構造システムとして用いる難易度の高さから、現代ではもっぱら芸術作品や玩具として用いられている。
ジェームズ・クラーク・マクスウェルは、自身の提案したトラス構造システムの静定次数と安定次数の計算式には適用範囲が存在し、これを適用できない特殊な形状が存在することを認めている。そのような形状は「何かしらの量を最大もしくは最小にするような特別な形状」であると述べている。テンセグリティはこの記述に合致するため、マクスウェルがテンセグリティを知っていたと解釈することもできる。(実際は直線上にならんだ直線部材などの単純な例を想定していたと考えられる)


